Article
21 janvier 2026
Article
En décembre, on fait le plein d'énergie chez Beneylu.🍊�...
Lire l’article
22 décembre 2025
Article
Votre programmation "Beneylu School Infini" de décembre sp�...
Lire l’article
12 décembre 2025
Article
Atterrissage en douceur après la rentrée. Beneylu School v...
Lire l’article
06 novembre 2025
Article
Voici votre programmation "Beneylu School Infini" d'octobre ...
Lire l’article
22 octobre 2025
Article
Retour sur le tourbillon de nouveautés de 2024-2025
Lire l’article
07 juillet 2025
Article
Vous êtes abonné à Beneylu School Infini, ce qui vous don...
Lire l’article
07 juillet 2025
Article
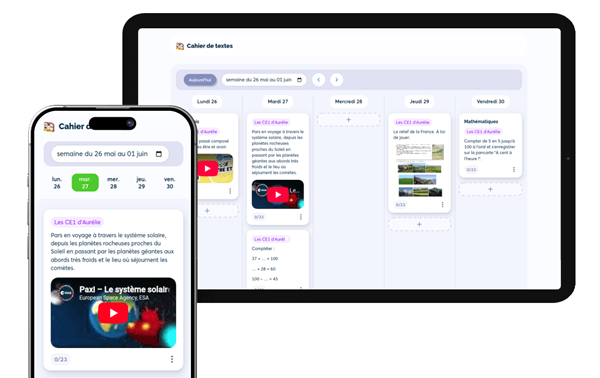
Le nouveau "cahier de textes" est ouvert aux classes volonta...
Lire l’article
07 juillet 2025
« Je peux travailler en toute confiance, le soutien est sans faille. La constance de la relation, le professionnalisme des équipes en face de moi ont fait de moi un utilisateur fidèle et indéfectible »
Article
En décembre, on fait le plein d'énergie chez Beneylu.🍊�...
Lire l’article
22 décembre 2025
Article
Votre programmation "Beneylu School Infini" de décembre sp�...
Lire l’article
12 décembre 2025
18 août 2025
Article
Atterrissage en douceur après la rentrée. Beneylu School v...
Lire l’article
06 novembre 2025
Article
Voici votre programmation "Beneylu School Infini" d'octobre ...
Lire l’article
22 octobre 2025
Article
Retour sur le tourbillon de nouveautés de 2024-2025
Lire l’article
07 juillet 2025
Article
Vous êtes abonné à Beneylu School Infini, ce qui vous don...
Lire l’article
07 juillet 2025
Article
Le nouveau "cahier de textes" est ouvert aux classes volonta...
Lire l’article
07 juillet 2025
« Je peux travailler en toute confiance, le soutien est sans faille. La constance de la relation, le professionnalisme des équipes en face de moi ont fait de moi un utilisateur fidèle et indéfectible »